Trigonometriya

Ang mga cosine at sine sa loob ng isang bilog na unit

Ang trigonometriya o trigonometrya (Bagong Latin: trigōnometria, mula sa Sinaunang Griyego: trígōnon "tatsulok" + -metron "pagsukat") o tatsihaan ay isang sangay ng matematika na isang pag-aaral ng mga tatsulok, partikular iyong mga tatsulok na plano (plane) na may sulok na 90 digri (right triangle o tamang tasulok) at ang mga kaugnayan sa pagitan ng mga gilid at ang ang mga anggulo ng mga gilid na ito. Ang trigonometriya ay naglalarawan din ng mga punsiyon na trigonometriko na ginagamit sa pagmomodelo o pag-unawa ng mga siklikal (paulit-ulit) na mga penomena sa kalikasan gaya ng mga alon (waves). Ang trigonometriya ay nabuo noong ikatlong siglo BCE bilang sangay ng heometriya at ito'y malawakang ginamit sa pag-aaral ng astronomiya. Ito rin ang pundasyon ng pagsusukat (surveying). Ang trigonometriya ay karaniwang itinuturo sa mga estudyante ng hayskul.

Konsepto

Sa tamang tatsulok (right triangle): Padron:Nowrap Padron:Nowrap Padron:Nowrap

Sa heometriya, ang isang anggulo ay isang pigura na nabubuo ng dalawang sinag (ray) ng pinagsasamang dulo ng tuldok (endpoint), na tinatawag na berteks (vertex) ng anggulo. Kung ang isa sa anggulo ng isang tatsulok ay may 90 na digri at ang isa pang anggulo ay alam, ang ikatlo ay matutukoy din, dahil ang tatlong mga anggulo ng anumang tatsulok ay binubuo ng 180 digri. Ang pinagsamang dalawang akyut na mga anggulo ay may sukat na 90 digri: ang tawag dito ay mga "komplementaryong mga anggulo". Ang hugis ng isang tatsulok ay ganap na matutukoy maliban sa pagkakapareho ng mga anggulo. Kapag alam ang mga anggulo, ang mga rasyo (ratio) ng mga gilid ay matutukoy kahit ano pa ang kabuuang sukat ng tatsulok. Kung ang haba ng isa sa mga gilid ay alam, ang dalawa pang gilid ay matutukoy. Sa kanang larawan, ipinapakita ang rasyo ng mga punsiyon na trigonometriko ng isang tatsulok kung saan ang anggulong A ay alam, at ang ang a, b at c ay tumutukoy sa haba ng mga gilid nito.

• sine (sin), ay tumutukoy sa rasyo ng kabaligtarang gilid (opposite side) ng isang anggulo sa gilis

$\sin A=\frac{\text{kabaligtaran(opposite)}}{\text{haypotenus(hypotenuse)}}=\frac{a}{c}.$

• cosine (cos), ay tumutukoy sa rasyo ng katabing gilid (adjacent side) sa gilis

$\cos A=\frac{\text{katabi(adjacent)}}{\text{haypotenus(hypotenuse)}}=\frac{b}{c}.$

• tangent (tan), ay tumutukoy sa rasyo ng kabaligtarang gilid (opposite side) sa katabing gilid (adjacent side)

$\tan A=\frac{\text{kabaligtaran(opposite)}}{\text{katabi(adjacent)}}=\frac{a}{b}=\frac{\sin A}{\cos A}.$

Pagpapalawig ng depinisyon

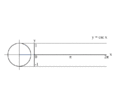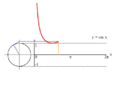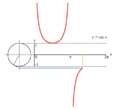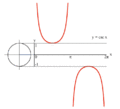
Ang mga depinisyon sa itaas ay inalalapat sa mga anggulo sa pagitan ng 0 at 90 digri (0 at π/2 radians) lamang. Kung gagamitin ang bilog na unit (unit circle), maaaring palawigin ang mga ito sa lahat ng positibo at negatibong argumento. Ang mga punsiyong trigonometriko ay periodiko na may period na 360 digi o 2π radians. Ang ibig sabihin nito, ang mga halaga nito ay umuulit sa mga interbal na ito. Ang tangent at cotangent ay may mas maikling period na 180 digri o π radian.

Ang mga punsiyong trigonometriko ay maaaring ilarawan sa ibang paraan bukod sa mga heometrikal na depinisyon sa itaas gamit ang mga kasangkapan sa kalkulo at inpinidong serye. Sa mga depinisyong ito, ang mga punsiyong trigonometriko ay maaaring ilarawan para sa mga bilang na kompleks. Ang eksponensiyal na kompleks na punsiyon ay partikular na magagamit.

$e^{x+iy}=e^x(\cos y+i\sin y).$

• 
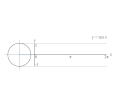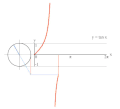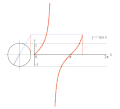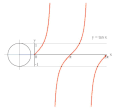
  Proseso ng pagga-grapo ng y = sin(x) gamit ang bilog na unit.
• 
  Proseso ng pagga-grapo ng y = tan(x) gamit ang bilog na unit.
• 
  Proseso ng pagga-grapo ng y = csc(x) gamit ang bilog na unit.

Mga Punsiyong inberso

Ang Inbersong (kabaligtarang) trigonometrikong mga punsiyon (inverse trigonometric functions o cyclometric functions) ang mga inberso (kabaligtaran) ng mga punsiyong trigonometriko na nagbibigay ng anggulo ng tatsulok. Kung paanong ang inberso ng ugat ng kwadrado (square root) $y=\sqrt{x}$ ay ang kwadrado (square) y² = x, ang inberso ng $\sin (\theta )=x$ ay $\arcsin (x)=\theta$ kung saan ang Θ ay kumakatawan sa isang anggulo ng tatsulok.

Ang tatlong karaniwang notasyon ng mga inbersyong punsiyong trigonometriko ay:

${\text{Sin}}^{-1}x=\theta ,\arcsin x=\theta ,\text{asin}x=\theta$,

${\text{Cos}}^{-1}x=\theta ,\arccos x=\theta ,\text{acos}x=\theta$

${\text{Tan}}^{-1}x=\theta ,\arctan x=\theta ,\text{atan}x=\theta$.

Maraming halaga ang ibinibigay ng sin(y) = x; halimbawa, ang sin(0) = 0, pati na rin ang sin(π) = 0, sin(2π) = 0, at iba pa. Samakatuwid ang punsiyong arcsine ay nagbibigay rin ng maraming halaga: arcsin(0) = 0, pati na rin arcsin(0) = π, arcsin(0) = 2π, at iba pa. Kung isang halaga lang ang ninanais, ang punsiyon ay hihigpitan lamang sa prinsipal na sangay. Sa restriksiyong ito, sa bawat x sa sakop (domain) ng ekspresyong arcsin(x), ito ay magdudulot lamang ng isang halaga na tinatawag na prinsipal na halaga. Ang katangiang ito ay lumalapat sa lahat ng inbersong punsiyong trigonometriko. Ang mga prinsipal na inberso ay nakatala sa sumusunod na tabla:

Pangalan	Usual na notasyon	Depinisyon	Sakop (domain) ng x sa real na resulta	Range sa karaniwang prinsipal na halaga (radian)	Range sa karaniwang prinsipal na halaga (digri)
arcsine	y = arcsin x	x = sin y	−1 ≤ x ≤ 1	−π/2 ≤ y ≤ π/2	−90° ≤ y ≤ 90°
arccosine	y = arccos x	x = cos y	−1 ≤ x ≤ 1	0 ≤ y ≤ π	0° ≤ y ≤ 180°
arctangent	y = arctan x	x = tan y	all real numbers	−π/2 < y < π/2	−90° < y < 90°
arccotangent	y = arccot x	x = cot y	all real numbers	0 < y < π	0° < y < 180°
arcsecant	y = arcsec x	x = sec y	x ≤ −1 or 1 ≤ x	0 ≤ y < π/2 or π/2 < y ≤ π	0° ≤ y < 90° or 90° < y ≤ 180°
arccosecant	y = arccsc x	x = csc y	x ≤ −1 or 1 ≤ x	−π/2 ≤ y < 0 or 0 < y ≤ π/2	-90° ≤ y < 0° or 0° < y ≤ 90°

Halimbawa ng praktikal na aplikasyon ng trigonometriya

Unang halimbawa

Ikaw ay nakatayo na may layong 20 talampakan mula sa paanan ng isang puno at nasukat mo ang anggulo ng elebasyon na 38 digri gamit ang isang instrumento (halimbawa clinometer o theodolite). Nais mong malaman ang taas ng puno ng hindi mo pisikal na susukatin ito.

Ang solusyon ay depende sa iyong taas habang sinusukat mo ang anggulo ng elebasyon mula sa linya ng paningin. Ipagpalagay nating ikaw ay may taas na 5 talampakan.

Ang larawan na ito ay nagpapakita ng tatsulok na ating nilulutas

Ang larawan sa kanan ay nagpapakita na pag nalaman na ang halaga ng T, kailangang magdagdag ng 5 talampakan sa halagang ito upang malaman ang kabuuang taas ng isang tatsulok. Upang malaman ang T kailangan nating gamitin ang punsiyong tangent:

$\tan (38^{\circ })=$	$\frac{\text{kabaligtaran (opposite)}}{\text{katabi (adjacent)}}=\frac{T}{20}$
$\tan (38^{\circ })=$	$\frac{T}{20}$
$T=$	$20\tan (38^{\circ })\approx 15.63$
$\text{taas ng puno}\approx$	$20.63\text{talampakan}$

Ikalawang halimbawa

Ang mundo, buwan at araw ay lumikha ng tamang tatsulok (right triangle) sa unang kwarter ng buwan. Ang layo ng mundo mula sa buwan ay 240,002.5 milya. Ano ang distansiya sa pagitan ng araw at buwan?

Gamitin natin ang d bilang distansiya sa pagitan ng araw at buwan. Maaari nating gamitin ang punsiyong tangent upang matukoy ang halaga ng d:

$\tan (89.85^{\circ })=$	$\frac{d}{240,002.5}$
$distansiya=$	$240,002.5\tan (89.85^{\circ })=91,673,992.71\text{milya}$

Karaniwang mga pormula

Ang identidad na trigonometriko ay tumutukoy sa mga ekwalidad (pagiging magkatumbas) ng mga ekspresyon ng mga punsiyon na trigonometriko na palaging totoo sa anumang halaga ng mga input gaya ng Θ at π na kumakatawan sa mga anggulo ng tatsulok. Halimbawa, sa anumang ibinigay na halaga ng Θ, ang resulta ng ekspresyong $\sec \theta$ ay palaging katumbas ng resulta ng ekspresyong $\frac{1}{\cos \theta }$. Ang mga identidad na trigonometriko ay ginagamit din upang lutasin/pasimplehin ang mga ekwasyon na trigonometriko sa termino ng isang punsiyon trigonometriko.

Mga resiprokal

Mga resiprokal ng cosine, sine, at tangent:

$\sec \theta =\frac{1}{\cos \theta },\csc \theta =\frac{1}{\sin \theta },\cot \theta =\frac{1}{\tan \theta }=\frac{\cos \theta }{\sin \theta }.$

Simetriya

Reflected in $\theta =0$	Reflected in $\theta =\pi /4$ (co-function identities)	Reflected in $\theta =\pi /2$
$\begin{array}{cc}\sin (-\theta )& =-\sin \theta \\ \cos (-\theta )& =+\cos \theta \\ \tan (-\theta )& =-\tan \theta \\ \csc (-\theta )& =-\csc \theta \\ \sec (-\theta )& =+\sec \theta \\ \cot (-\theta )& =-\cot \theta \end{array}$	$\begin{array}{cc}\sin (\frac{\pi }{2}-\theta )& =+\cos \theta \\ \cos (\frac{\pi }{2}-\theta )& =+\sin \theta \\ \tan (\frac{\pi }{2}-\theta )& =+\cot \theta \\ \csc (\frac{\pi }{2}-\theta )& =+\sec \theta \\ \sec (\frac{\pi }{2}-\theta )& =+\csc \theta \\ \cot (\frac{\pi }{2}-\theta )& =+\tan \theta \end{array}$	$\begin{array}{cc}\sin (\pi -\theta )& =+\sin \theta \\ \cos (\pi -\theta )& =-\cos \theta \\ \tan (\pi -\theta )& =-\tan \theta \\ \csc (\pi -\theta )& =+\csc \theta \\ \sec (\pi -\theta )& =-\sec \theta \\ \cot (\pi -\theta )& =-\cot \theta \\ \end{array}$

Peryodisidad

Shift by π/2	Shift by π Period for tan and cot	Shift by 2π Period for sin, cos, csc and sec
$\begin{array}{cc}\sin (\theta +\frac{\pi }{2})& =+\cos \theta \\ \cos (\theta +\frac{\pi }{2})& =-\sin \theta \\ \tan (\theta +\frac{\pi }{2})& =-\cot \theta \\ \csc (\theta +\frac{\pi }{2})& =+\sec \theta \\ \sec (\theta +\frac{\pi }{2})& =-\csc \theta \\ \cot (\theta +\frac{\pi }{2})& =-\tan \theta \end{array}$	$\begin{array}{cc}\sin (\theta +\pi )& =-\sin \theta \\ \cos (\theta +\pi )& =-\cos \theta \\ \tan (\theta +\pi )& =+\tan \theta \\ \csc (\theta +\pi )& =-\csc \theta \\ \sec (\theta +\pi )& =-\sec \theta \\ \cot (\theta +\pi )& =+\cot \theta \\ \end{array}$	$\begin{array}{cc}\sin (\theta +2\pi )& =+\sin \theta \\ \cos (\theta +2\pi )& =+\cos \theta \\ \tan (\theta +2\pi )& =+\tan \theta \\ \csc (\theta +2\pi )& =+\csc \theta \\ \sec (\theta +2\pi )& =+\sec \theta \\ \cot (\theta +2\pi )& =+\cot \theta \end{array}$

Sine at cosine ng mga suma ng walang hangganang termino

$\sin \left(\sum _{i=1}^{\mathrm{\infty }}{\theta }_i\right)=\sum _{\text{odd}k\ge 1}(-1{)}^{(k-1)/2}\sum _{\begin{array}{c}A\subseteq \{1,2,3,\dots \}\\ \left|A\right|=k\end{array}}(\prod _{i\in A}\sin {\theta }_i\prod _{i\in ̸A}\cos {\theta }_i)$

$\cos \left(\sum _{i=1}^{\mathrm{\infty }}{\theta }_i\right)=\sum _{\text{even}k\ge 0}(-1{)}^{k/2}\sum _{\begin{array}{c}A\subseteq \{1,2,3,\dots \}\\ \left|A\right|=k\end{array}}(\prod _{i\in A}\sin {\theta }_i\prod _{i\in ̸A}\cos {\theta }_i)$

Tangent ng mga suma ng walang hangganang termino

$\begin{array}{cc}{e}_0& =1\\ e_1& =\sum _{1\le i\le n}{x}_i& & =\sum _{1\le i\le n}\tan {\theta }_i\\ e_2& =\sum _{1\le i<j\le n}{x}_i{x}_j& & =\sum _{1\le i<j\le n}\tan {\theta }_i\tan {\theta }_j\\ e_3& =\sum _{1\le i<j<k\le n}{x}_i{x}_j{x}_k& & =\sum _{1\le i<j<k\le n}\tan {\theta }_i\tan {\theta }_j\tan {\theta }_k\\ & ⋮& & ⋮\end{array}$

Secant at cosecant ng mga suma ng walang hangganang termino

$\begin{array}{cc}\sec ({\theta }_1+\cdots +{\theta }_n)& =\frac{\sec {\theta }_1\cdots \sec {\theta }_n}{e_0-e_2+e_4-\cdots }\\ \csc ({\theta }_1+\cdots +{\theta }_n)& =\frac{\sec {\theta }_1\cdots \sec {\theta }_n}{e_1-e_3+e_5-\cdots }\end{array}$

Then

$\tan ({\theta }_1+\cdots +{\theta }_n)=\frac{e_1-e_3+e_5-\cdots }{e_0-e_2+e_4-\cdots },$

Mga katumbas na punsiyon sa termino ng iba pang punsiyon

Mga katumbas na punsiyon sa termino ng iba pang punsiyon

in terms of	$\sin \theta$	$\cos \theta$	$\tan \theta$	$\csc \theta$	$\sec \theta$	$\cot \theta$
$\sin \theta =$	$\sin \theta$	$\pm \sqrt{1-{\cos }^2\theta }$	$\pm \frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}$	$\frac{1}{\csc \theta }$	$\pm \frac{\sqrt{{\sec }^2\theta -1}}{\sec \theta }$	$\pm \frac{1}{\sqrt{1+{\cot }^2\theta }}$
$\cos \theta =$	$\pm \sqrt{1-{\sin }^2\theta }$	$\cos \theta$	$\pm \frac{1}{\sqrt{1+{\tan }^2\theta }}$	$\pm \frac{\sqrt{{\csc }^2\theta -1}}{\csc \theta }$	$\frac{1}{\sec \theta }$	$\pm \frac{\cot \theta }{\sqrt{1+{\cot }^2\theta }}$
$\tan \theta =$	$\pm \frac{\sin \theta }{\sqrt{1-{\sin }^2\theta }}$	$\pm \frac{\sqrt{1-{\cos }^2\theta }}{\cos \theta }$	$\tan \theta$	$\pm \frac{1}{\sqrt{{\csc }^2\theta -1}}$	$\pm \sqrt{{\sec }^2\theta -1}$	$\frac{1}{\cot \theta }$
$\csc \theta =$	$\frac{1}{\sin \theta }$	$\pm \frac{1}{\sqrt{1-{\cos }^2\theta }}$	$\pm \frac{\sqrt{1+{\tan }^2\theta }}{\tan \theta }$	$\csc \theta$	$\pm \frac{\sec \theta }{\sqrt{{\sec }^2\theta -1}}$	$\pm \sqrt{1+{\cot }^2\theta }$
$\sec \theta =$	$\pm \frac{1}{\sqrt{1-{\sin }^2\theta }}$	$\frac{1}{\cos \theta }$	$\pm \sqrt{1+{\tan }^2\theta }$	$\pm \frac{\csc \theta }{\sqrt{{\csc }^2\theta -1}}$	$\sec \theta$	$\pm \frac{\sqrt{1+{\cot }^2\theta }}{\cot \theta }$
$\cot \theta =$	$\pm \frac{\sqrt{1-{\sin }^2\theta }}{\sin \theta }$	$\pm \frac{\cos \theta }{\sqrt{1-{\cos }^2\theta }}$	$\frac{1}{\tan \theta }$	$\pm \sqrt{{\csc }^2\theta -1}$	$\pm \frac{1}{\sqrt{{\sec }^2\theta -1}}$	$\cot \theta$

Teorema ni Pitagorean

${\sin }^{2}A+{\cos }^{2}A=1$

${\sec }^{2}A-{\tan }^{2}A=1$

${\csc }^{2}A-{\cot }^{2}A=1$

Mga katumbas na suma at subtraksiyon sa termino ng ibang punsiyon

Sine	$\sin (\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$
Cosine	$\cos (\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta$
Tangent	$\tan (\alpha \pm \beta )=\frac{\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }$
Arcsine	$\arcsin \alpha \pm \arcsin \beta =\arcsin (\alpha \sqrt{1-{\beta }^2}\pm \beta \sqrt{1-{\alpha }^2})$
Arccosine	$\arccos \alpha \pm \arccos \beta =\arccos (\alpha \beta \mp \sqrt{(1-{\alpha }^2)(1-{\beta }^2)})$
Arctangent	$\arctan \alpha \pm \arctan \beta =\arctan \left(\frac{\alpha \pm \beta }{1\mp \alpha \beta }\right)$

Doble-, triple-, at kalahating-anggulo

Doble-anggulo
$\begin{array}{cc}\sin 2\theta & =2\sin \theta \cos \theta \\ & =\frac{2\tan \theta }{1+{\tan }^2\theta }\end{array}$	$\begin{array}{cc}\cos 2\theta & ={\cos }^2\theta -{\sin }^2\theta \\ & =2{\cos }^2\theta -1\\ & =1-2{\sin }^2\theta \\ & =\frac{1-{\tan }^2\theta }{1+{\tan }^2\theta }\end{array}$	$\tan 2\theta =\frac{2\tan \theta }{1-{\tan }^2\theta }$	$\cot 2\theta =\frac{{\cot }^2\theta -1}{2\cot \theta }$
Triple-anggulo
$\begin{array}{cc}\sin 3\theta & =3{\cos }^2\theta \sin \theta -{\sin }^3\theta \\ & =3\sin \theta -4{\sin }^3\theta \end{array}$	$\begin{array}{cc}\cos 3\theta & ={\cos }^3\theta -3{\sin }^2\theta \cos \theta \\ & =4{\cos }^3\theta -3\cos \theta \end{array}$	$\tan 3\theta =\frac{3\tan \theta -{\tan }^3\theta }{1-3{\tan }^2\theta }$	$\cot 3\theta =\frac{3\cot \theta -{\cot }^3\theta }{1-3{\cot }^2\theta }$
Kalahating-anggulo
$\sin \frac{\theta }{2}=\pm \sqrt{\frac{1-\cos \theta }{2}}$	$\cos \frac{\theta }{2}=\pm \sqrt{\frac{1+\cos \theta }{2}}$	$\begin{array}{cc}\tan \frac{\theta }{2}& =\csc \theta -\cot \theta \\ & =\pm \sqrt{\frac{1-\cos \theta }{1+\cos \theta }}\\ & =\frac{\sin \theta }{1+\cos \theta }\\ & =\frac{1-\cos \theta }{\sin \theta }\\ \tan \frac{\eta +\theta }{2}& =\frac{\sin \eta +\sin \theta }{\cos \eta +\cos \theta }\\ \tan (\frac{\theta }{2}+\frac{\pi }{4})& =\sec \theta +\tan \theta \\ \sqrt{\frac{1-\sin \theta }{1+\sin \theta }}& =\frac{1-\tan (\theta /2)}{1+\tan (\theta /2)}\end{array}$	$\begin{array}{cc}\cot \frac{\theta }{2}& =\csc \theta +\cot \theta \\ & =\pm \sqrt{\frac{1+\cos \theta }{1-\cos \theta }}\\ & =\frac{\sin \theta }{1-\cos \theta }\\ & =\frac{1+\cos \theta }{\sin \theta }\end{array}$

Pagbawas kapangyarihan

Sine	Cosine	Other
${\sin }^2\theta =\frac{1-\cos 2\theta }{2}$	${\cos }^2\theta =\frac{1+\cos 2\theta }{2}$	${\sin }^2\theta {\cos }^2\theta =\frac{1-\cos 4\theta }{8}$
${\sin }^3\theta =\frac{3\sin \theta -\sin 3\theta }{4}$	${\cos }^3\theta =\frac{3\cos \theta +\cos 3\theta }{4}$	${\sin }^3\theta {\cos }^3\theta =\frac{3\sin 2\theta -\sin 6\theta }{32}$
${\sin }^4\theta =\frac{3-4\cos 2\theta +\cos 4\theta }{8}$	${\cos }^4\theta =\frac{3+4\cos 2\theta +\cos 4\theta }{8}$	${\sin }^4\theta {\cos }^4\theta =\frac{3-4\cos 4\theta +\cos 8\theta }{128}$
${\sin }^5\theta =\frac{10\sin \theta -5\sin 3\theta +\sin 5\theta }{16}$	${\cos }^5\theta =\frac{10\cos \theta +5\cos 3\theta +\cos 5\theta }{16}$	${\sin }^5\theta {\cos }^5\theta =\frac{10\sin 2\theta -5\sin 6\theta +\sin 10\theta }{512}$

	Cosine	Sine
$\text{if }n\text{ is odd}$	${\cos }^n\theta =\frac{2}{2^n}\sum _{k=0}^{\frac{n-1}{2}}(\genfrac{}{}{0ex}{}{n}{k})\cos ((n-2k)\theta )$	${\sin }^n\theta =\frac{2}{2^n}\sum _{k=0}^{\frac{n-1}{2}}(-1{)}^{(\frac{n-1}{2}-k)}(\genfrac{}{}{0ex}{}{n}{k})\sin ((n-2k)\theta )$
$\text{if }n\text{ is even}$	${\cos }^n\theta =\frac{1}{2^n}(\genfrac{}{}{0ex}{}{n}{\frac{n}{2}})+\frac{2}{2^n}\sum _{k=0}^{\frac{n}{2}-1}(\genfrac{}{}{0ex}{}{n}{k})\cos ((n-2k)\theta )$	${\sin }^n\theta =\frac{1}{2^n}(\genfrac{}{}{0ex}{}{n}{\frac{n}{2}})+\frac{2}{2^n}\sum _{k=0}^{\frac{n}{2}-1}(-1{)}^{(\frac{n}{2}-k)}(\genfrac{}{}{0ex}{}{n}{k})\cos ((n-2k)\theta )$

Produkto-sa-suma at suma-sa-produkto

Product-to-sum $\cos \theta \cos \phi =\frac{\cos (\theta -\phi )+\cos (\theta +\phi )}{2}$ $\sin \theta \sin \phi =\frac{\cos (\theta -\phi )-\cos (\theta +\phi )}{2}$ $\sin \theta \cos \phi =\frac{\sin (\theta +\phi )+\sin (\theta -\phi )}{2}$ $\cos \theta \sin \phi =\frac{\sin (\theta +\phi )-\sin (\theta -\phi )}{2}$

Sum-to-product $\sin \theta \pm \sin \phi =2\sin \left(\frac{\theta \pm \phi }{2}\right)\cos \left(\frac{\theta \mp \phi }{2}\right)$ $\cos \theta +\cos \phi =2\cos \left(\frac{\theta +\phi }{2}\right)\cos \left(\frac{\theta -\phi }{2}\right)$ $\cos \theta -\cos \phi =-2\sin \left(\frac{\theta +\phi }{2}\right)\sin \left(\frac{\theta -\phi }{2}\right)$

Walang hangganang produkto

$\sin x=x\prod _{n=1}^{\mathrm{\infty }}(1-\frac{x^2}{{\pi }^2{n}^2})$

$\sinh x=x\prod _{n=1}^{\mathrm{\infty }}(1+\frac{x^2}{{\pi }^2{n}^2})$

$\frac{\sin x}{x}=\prod _{n=1}^{\mathrm{\infty }}\cos \left(\frac{x}{2^n}\right)$

$\cos x=\prod _{n=1}^{\mathrm{\infty }}(1-\frac{x^2}{{\pi }^2(n-\frac{1}{2}{)}^2})$

$\cosh x=\prod _{n=1}^{\mathrm{\infty }}(1+\frac{x^2}{{\pi }^2(n-\frac{1}{2}{)}^2})$

$|\sin x|=\frac{1}{2}\prod _{n=0}^{\mathrm{\infty }}\sqrt[2^{n+1}]{|\tan \left(2^{n}x\right)|}$

Pormula ni Euler

Ang pormula ni Euler na nagsasaad na $e^{ix}=\cos x+i\sin x$ ay lumilikha ng mga sumusunod na identidad na analitikal para sa sine, cosine at tangent sa termino ng e at imahinaryong unit na i:

$\sin x=\frac{e^{ix}-e^{-ix}}{2i},\cos x=\frac{e^{ix}+e^{-ix}}{2},\tan x=\frac{i(e^{-ix}-e^{ix})}{e^{ix}+e^{-ix}}.$

Pagtukoy ng mga gilid at anggulo

Ang mga anggulong α, β, at γ ay kabalagitaran ng mga gilid na a, b, and c.

Batas ng mga sine

Ang batas ng mga sine (law of sines) ay ginagamit upang kwentahin ang mga natitirang gilid kung ang dalawang anggulo at isang gilid ay alam. Ito ay ginagamit rin kung ang dalawang gilid at ang anggulo sa pagitan nito ay alam. Sa ibang kaso, ang pormula ay nagbibigay ng dalawang posibleng halaga sa anggulo sa pagitan ng dalawang gilid.

$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R,$

kung saan ang R ang radyus ng bilog na sirkumskribo (bilog na dumadaan sa lahat ng berteks ng isang tatsulok):

$R=\frac{abc}{\sqrt{(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}.$

Isa pang batas kaugnay ng sine ay maaaring gamitin upang kwentahin ang isang area ng isang tatsulok. Kung ang dalawang mga gilid at isang anggulo sa pagitan ng mga gilid na ito ay ibinigay, ang area ng tatsulok ay:

$\text{Area}=\frac{1}{2}ab\sin C.$

Lahat ng mga punsiyong trigonometriko ng isang anggulong tinatawag na θ ay maaaring likhain sa termino ng isang bilog na unit (unit circle) sa O.

Batas ng mga cosine

Ang batas ng mga cosine (law of cosines) ay isang ektensiyon ng Teorema ni Pitagoras sa anumang napiling sukat na tatsulok. Ang batas ng cosine ay ginagamit upang malaman ang ikatlong gilid kung ang dalawang gilid at ang ang anggulo sa pagitan ng dalawang gilid na ito ay alam.

$c^2=a^2+b^2-2ab\cos \gamma$

$a^2=b^2+c^2-2bc\cos \alpha$

$b^2=a^2+c^2-2ac\cos \beta$

Ang inibang anyo ng batas ng cosine ay ginagamit upang malaman ang mga anggulo ng isang tatsulok kung ang lahat ng gilid nito ay alam.

$\cos \gamma =\frac{a^2+b^2-c^2}{2ab}$

$\cos \alpha =\frac{b^2+c^2-a^2}{2bc}$

$\cos \beta =\frac{c^2+a^2-b^2}{2ca}$

Batas ng mga tangent

Ang batas ng mga tangent (law of tangents) ay maaaring gamitin upang matukoy ang isang gilid o anggulo kung ang dalawang gilid at isang anggulo na hindi kasama o dalawang anggulo at isang gilid ay alam.

$\frac{a-b}{a+b}=\frac{\tan [\frac{1}{2}(A-B)]}{\tan [\frac{1}{2}(A+B)]}$

Halimbawa ng paglutas ng trigonometrikong ekwasyon

Para lutasin ang bariabulo na x sa ekwasyong nasa anyong $a\sin x+b\cos x=c$ kung saan ang a, b, at c ay konstante, gagamit tayo ng identidad na trigonometriko na:

$a\sin x+b\cos x=\sqrt{a^2+b^2}\sin (x+\alpha )$

Para malaman ang halaga ng anggulong $\alpha$ gagamit tayo ng arctangent:

$\alpha =\{\begin{array}{cc}{\tan }^{-1}(b/a),& \text{if }a>0\\ \pi +{\tan }^{-1}(b/a),& \text{if }a<0\end{array}$

Ang ekwasyon ay naging:

$\sqrt{a^2+b^2}\sin (x+\alpha )=c$

Pansinin na ang ekwasyon ay pinasimple dahil sa paghalili ng identidad sa termino ng isa lamang punsiyon na trigonometriko. Sa kasong ito ay sa punsiyong sine (sin) na lamang.

Ngayon, hatiin (divide) ang parehong panig ng ekspresyon, ng :$\sqrt{a^2+b^2}$

$\sin (x+\alpha )=\frac{c}{\sqrt{a^2+b^2}}$

Ang ekwasyon ito ay nasa anyong $\sin x=n$ na ang mga solusyon ay:

$x=\alpha +2k\pi$

$x=\pi -\alpha +2k\pi$

kung saan ang :$\alpha ={\sin }^{-1}n$ at ang $k$ ay isang intedyer.

Halimbawa, lulutasin natin ito:

$\sin 3x-\sqrt{3}\cos 3x=-\sqrt{3}$

Sa kasong ito, meron tayong:

$a=1,b=-\sqrt{3},c=-\sqrt{3}$

$\sqrt{a^2+b^2}=\sqrt{1^2+{(-\sqrt{3})}^2}=2$

$\alpha ={\tan }^{-1}(-\sqrt{3})=-\frac{\pi }{3}$

Ilapat ang nasa taas sa identidad na trigonometriko na $\sqrt{a^2+b^2}\sin (x+\alpha )$

Ang ekwasyong $\sin 3x-\sqrt{3}\cos 3x=-\sqrt{3}$ ay naging $\sqrt{a^2+b^2}\sin (x+\alpha )=c$

$2\sin (3x-\frac{\pi }{3})=-\sqrt{3}$

Ngayon, hatiin (divide) ang parehong panig ng ekspresyon, ng :$2$

$\sin (3x-\frac{\pi }{3})=-\frac{\sqrt{3}}{2}$

Kung gagamitin natin ang pormula na $\sin x=n$, ang mga solusyon ng orihinal na ekwasyong $\sin 3x-\sqrt{3}\cos 3x=-\sqrt{3}$ ay:

$3x-\frac{\pi }{3}=-\frac{\pi }{3}+2k\pi \iff x=\frac{2k\pi }{3}$

$3x-\frac{\pi }{3}=\pi +\frac{\pi }{3}+2k\pi \iff x=\frac{\pi }{9}(6k+5)$

kung saan ang $k$ ay isang intedyer.